
Xin ba.n ddo.c go'p y' the^m dde^? cho ba`i na`y dduo+.c hoa`n chi?nh ho+n. Xin ddu+`ng e nga.i dda(.t ca^u ho?i. Email to^i la` trieuvan@yahoo.com. Xin thu+' lo^~i vi` to^i co' du`ng mo^.t so^' tu+` anh ngu+~ la^~n lo^.n

La`m cho ma'y dda'nh co+` kho^ng pha?i la` kho', nhu+ng ra^'t to^'n tho+`i gian. Bu` la.i sau khi ma'y dda'nh dduo+.c so+ so+, khi cho+i vo+'i no' ra^'t la` dda~. No' ddi nhie^`u nuo+'c ngu, nhu+ng mi`nh la.i thua vi` nhu+~ng nuo+'c ngu na`y mo+'i che^'t ! Mi`nh pha?i ca?i tie^'n no' kho^ng ngu+`ng, vi` kho^ng bao gio+` no' co' the^? la`m cho mi`nh ha`i ca?.
To^i ddang vie^'t mo^.t program thu+? nghie^.m go.i la` thangngo, no' dda'nh cu~ng dduo+.c. DDo^i khi to^i cu~Ng bi. no' bu.p :-)
Mu.c tie^u chi'nh la` la` la`m sao ta.o dduo+.c mo^.t ca^'u tru'c du+~ lie^.u dde^? khi thu+.c hie^.n ca'c thao ta'c sau nhanh nha^'t, vi` ca'c thao ta'c na`y la^.p ddi la^.p la.i ra^'t nhie^`u la^`n.
- DDi mo^.t nuo+'c (make move) va` hoa`ni la.i nuo+'c ddi ddo' (unmake move).
- Pha't sinh ta^'t ca? ca'c nuo+'c ddi (dde^? ta.o game tree)
- DDa'nh gia' gia'tri. ti~nh cu?a ba.n co+`.
Ba`n co+` truo+'ng go^`m 9x10 vi. tri', ta co' the^? chu+'a ba`n co+` trong mo^.t array mo^.t chie^`u ki'ch thuo+'c 9x10. Mo^.t nuo+'c ddi ca^`n 2 byte dde^? chu+'a vi. tri' dda^`u va` vi. tri' cuo^'i cu?a nuo+'c ddi. Nhu+ng co`n ke.t ca'i la` khi la`m the^' na`o dde^? tra'nh mo^.t qua^n ddi ra kho?i ba`n co+`. Co' nhie^`u phuo+ng pha'o nhu+ng to^i dde^` nghi. mo^.t phuo+ng pha'p la` mi`nh cho the^m 1 ha`ng o+? chie^`u do.c va` 2 ha`ng o+? chie^`u ngang dde^? tie^.n ca'ch ti'nh ti'nh toa'n.
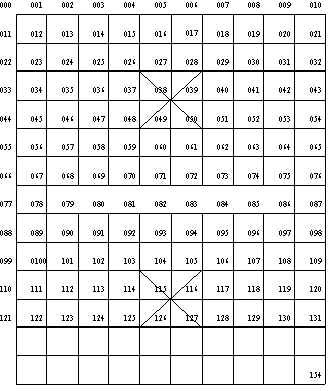
Nhu+ hi`nh tre^n xe ddo? se~ o+? vi. tri' 23,31. ma~ o+? 24,30 v.v ca'c o^ hai ha`ng dda^`u (0->21), va` co^.t dda^u` (22,33, v.v) co^.t cuo^'i (32,43,v.v) se~ dduo+.c ga'n nhu+~ng gia' tri. dda(.c bie^.t dde^? ba'o dda~ ngoa`i ba`n co+`.
Ba(`ng ca'ch na`y mi`nh khi pha't sinh ta^'t ca? ca'c nuo+'c ddi cho 1 qua^n ra^'t la` ddo+n gia?n. Gia? su+? 1 qua^n ddang ddu+'ng o+? o^ n: qua^n na`y ddi ngang la` n+d hay n-d, ddi do.c la` n+11*d hay la` n-11*d, ddi nhu+ ma~ (n-23),(n-21) v.v. Ne^'u o^ mo+'i kho^ng ngoa`i ba`n co+` thi` nuo+'c ddi ddo' mo+'i ho+.p le^.
Trong qua' tri`nh pha't sinh ca'c nuo+'c, mi`nh pha?i cha('c cha('n tuo+'ng kho^ng bi. chie^'u. Kie^?m tra ca'c na`y ra^'t to^'n tho+`i gio+`. To^i ddang suy nghi~ la`m sao pha't sinh ca'c nuo+'c ddi tha^.t nhanh. Any idea ???
Gia' tri. ba`n co+` thuo+`ng dduo+.c ti'nh theo:
Gia' tri. cu?a qua^n: Xe = 900 Pha'o = 450 Ma~ = 400 Si~ = 200 Tuo+.ng =200. To^'t ba(`ng 100 ne^'u chu+a qua so^ng, co`n qua so^ng thi` mi`nh cho no' 200.
Ca'ch dda'nh gia' tre^n ra^'t tuo+ng ddo^'i vi` o+? co+` ta`n thi` ma~ thuo+`ng ma.nh ho+n pha'o, to^'t nha^.p cung cu~ng cha(?ng ke'm gi` xe v.v
Mo^.t dde^` nghi. la` tre^n tu+`ng vi. tri' cu?a ba`n co+` qua^n se~ co' tu+`ng gia' tri. kha'c nhau. DDa^y chi'nh la` c ca'ch ma` thangngo la`m. Nhu+ng gia' tri. tre^n tu+`ng o^ cu?a qua^n la` bao nhie^u th`i ddang co`n suy nghi~ :-)
Su+. linh ddo^.ng cu?a ca'c qua^n: Ca'c qua^n thuo+`ng pha?i thoa'ng, co' nhie^`u nuo+'c ddi th`i dduo+ng nhie^n to^'t ho+n nhu+ng ca'i na`y ra^'t la` kho' ddu+a va`o program. Thangngo mo+'i ti'nh dde^'n su+. linh ddo^.ng cu?a xe ma~ tho^i, chu+a bie^'t la`m sao dda'nh su+. linh ddo^.ng cu?a pha'o.
Su+. ke^'t ho+.p giu+~a ca'c qua^n: Mo^.t so^' ca'ch ke^'t ho+.p thuo+`ng ga(.p: Pha'o gia(ng, ma~ giao cha^n, to^'t ca(.p ke` v.v ne^n dduo+.c the^m ddie^?m.
The^': The^' cu~ng ra^'t quan tro.ng, cha(?ng ha.n nhu+ mi`nh co' pha'o dda^`u hay pha'o tro^'ng thi` ra^'t co' lo+.i cho the^' co^ng.
Co`n gi` nu+~a kho^ng ??.....
Khi ti'nh mo^.t nuo+'c ddi thi` mi`nh thu+? ddi nuo+'c ddo' xem co' lo+.i hai kho^ng so vo+'i nhu+~ng nuo+'c kha'c. Tti'nh truo+'c 1 nuo+'c tu+'c la` mi`nh ddi thu+? 1 nuo+'c xem co' lo+.i hay kho^ng ? Ti'nh truo+'c n nuo+'c tu+'c la` mi`nh ddi thu+? n/2 nuo+'c va` ddo^'i phuo+ng ddi thu+? n/2 nuo+'c.
Qua' tri`nh na`y ta.o tha`nh 1 ca'i tree, co' depth la` n. O+? mo^~i node tre^n tre^n se~ co' gia' tri. ba(`ng chi'nh no' ne^'u no' la` leaf, co`n kho^ng thi` gia' tri. no' se~ la` max cu?a ca'c children ne^'u dde^'n mi`nh ddi, va` la` min ne^'u ddi.ch thu? ddi (bo+?i vi` ai cu~ng muo^'n cho.n nuo+'c to^'t nha^'t cho mi`nh, ma` nuo+'c to^'t nha^'t cu?a ddi.ch thu? la` nuo+'c te^. nha^'t cu?a mi`nh). Ca'i tree na`y go.i la` minimax tree.
Sau dda^y la` 1 ddoa.n code dde^? dda'nh gia' minimax tree:
int minimax(int depth)
{
if (depth <= 0 || game is over) return eval(banco);
else {
int result = -infinity;
for (mo.i nuo+'c ddi m cu?a banco) {
make move m;
result = max(result,
-minimax(depth - 1));
unmake move m;
}
return result;
}
}
Thua^.t toa'n tre^n hoa`n toa`n ddu'ng, nhu+ng co' ddie^`u cha^.m, mi`nh co' the^? la`m nhanh ho+n the^'. Ha~y xem hi`nh duo+'i na`y:
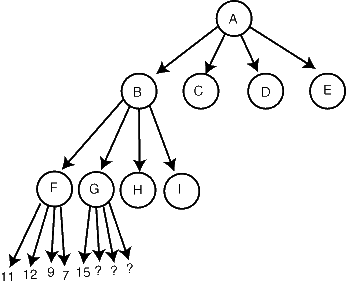
O+? node F mi`nh cho.n gia' tri. lo+'n nha^'t la` 12, Lu'c to+'i G gia' tri. cu?a no' la` 15 hay lo+'n ho+n nu+~a nhu+ng mi`nh kho^ng ca^`n quan ta^m dde^'n no' nu+~a bo+?i vi` B se~ cho.n gia' tri. min nho? ho+n 12 ne^n kho^ng bao gio+` cho.n G. Chu'ng ta co' the^? loa.i bo? G (Ca'i na`y go.i la` prunning) Tu+` dda^y ddu+a to+'i mo^.t thua^.t toa'n mo+'i go.i la` alphabeta.
Trong alphabeta mi`nh chi? quan ta^m dde^'n gia' tri. cu?a nhu+~ng node na`o nho? ho+n ca'i cha(.n tre^n la` beta ma` tho^i. alpha ddo'ng vai tro` cha(.n duo+'i, no' la` ca'i to^'t nha^'t dda~ ti`m dduo+.c. Lu'c dde^'n ddo^'i phuo+ng ddi thi` cha(.n duo+'i cu?a mi`nh tha`nh cha(.n tre^n cu?a ho. va` nguo+.c la.i.
int alphabeta(int depth,int alpha,int beta)
{
if (depth <= 0 || game is over) return eval(banco);
else {
ta.o ra mo.i nuo+'c, va` sa('p xe^'p ca'c
nuo+'c ddi na`y.
for (mo.i nuo+'c ddi m cu?a banco) {
make move m;
val = -alphabeta(depth
- 1,-beta,-alpha); // (*)
unmake move m;
if (val>=beta)
return val;
if (val>alpha)
alpha=val;
}
return alpha;
}
}
Chu' y ': Buo+'c sa('p xe^'p ca'c nuo+'c ddi ra^'t la` quan tro.ng. Nguo+`i ta chu+'ng minh dduo+.c la` mi`nh ddi nuo+'c na`o to^'t nha^'t (theo nghi~a tuo+ng ddo^'i) truo+'c thi` se~ la`m tree dduo+.c ca('t bo? nhie^`u nha^'t. Nhu+ng ne^'u mi`nh la`m buo+'c sa('p xe^'p na`y phu+'c ta.p qua' thi` la.i to^'n tho+`i gio+` vo^ buo+'c na`y la`m thua^.t toa'n cha.y cha^.m la.i.
Ve^ gia' tri. ban dda^`u cu?a alpha, beta thuo+`ng thi` no' la` (-infinity,+infinity) nhu+ng ne^'u ne^'u mi`nh cho ca'i window na`y nho? ho+n thi` search se~ mau ho+n, nhu+ng ne^'u mi`nh dde^? khoa?ng ca'ch na`y qua' nho?, gia' tri. thu+.c su+. cu?a tree na(`m ngoa`i (alpha,beta) thi` alphabeta se~ tra? ve^` sai ke^'t qua? :-)
(*) Thay vi` val = -alphabeta(depth - 1,-beta,-alpha) ba.n co' the^? thay ba(`ng:
val =
-alphabeta(depth - 1,-alpha,-alpha); // test xem gia' tri. cu?a val lo+'n ho+n
alpha kho^ng ???
if (val>=alpha)
val = -alphabeta(depth - 1,-beta,-alpha);
Phuo+ng pha'p na`y thuo+`ng la`m cho program cha.y nhanh ho+n nhie^`u.
Nhie^`u khi mi`nh ti'nh truo+'c n nuo+'c, mi`nh se~ kho^ng tha^'y dduo+.c nuo+'c ma^'t xe, hay bi. chie^'u bi' o+? nuo+'c n+1, ca'i na`y go.i la` horizon effect. DDe^? gia?i quye^'t cho^~ na`y sau khi ti'nh to+'i leaf cu?a tree mi`nh co' the^? ti'nh the^m mo^.t va`i nuo+'c, cho dde^'n khi ba`n co+` o^?n ddi.nh (quiescene). Nhu+~ng truo+`ng ho+.p sau mi`nh ne^n ti'nh the^m:
A(n qua^n: Ne^'u ma` o+? leaf co' the^? a(n dduo+.c qua^n ddo^'i phuo+ng thi` gia' tri. cu?a tree bi. thay ddo^?i ra^'t nhie^`u, cho ne^n mi`nh ne^n thu+? nhu+~ng nuo+'c a(n qua^n. Nhu+ng nhu+~ng nuo+'c na`y kho^ng pha?i ba('t buo^.c. Cha(?ng ha.n nhu+ mi`nh co' the^? du`ng xe a(n ma~, nhu+ng sau ddi.ch thu? nguo+`i ta a(n la.i xe mi`nh thi` ro~ ra`ng la` a(n ma~ chu+a ha(?n la` to^'t.
Bi. chie^'u: Thuo+`ng khi mi`nh bi. chie^'u mi`nh pha?i co^' ga('ng thoa't kho?i ti`nh tra.ng na`y thi` dda'nh gia' ba`n co+` mo+'i chi'nh xa'c.
Ne^'u mi`nh dde^? ddo^'i phuo+ng ddi hai nuo+'c mo^.t lu'c thi` mi`nh kho^ng bao gio+`tha('ng dduo+.c ddo^'i, nguo+.c la.i ne^'u mi`nh ma` ddi hai nuo+'c ma` mi`nh kho^ng la`m gi` dduo+.c ddo^'i phuo+ng thi` ti`nh tra.ng cu?a mi`nh ddang to^`i te^.. Ra^'t hie^'m khi mi`nh kho^ng co' nuo+'c ddi pha?i dde^? ddo^'u phuo+ng ddi the^m nuo+'c nu+~a (nhu+ng truo+`ng ho+.p na`y co' chu+' kho^n g pha?i kho^ng).
Mo^.t ca'ch dde^? test coi ti`nh tra.ng ba`n la` mi`nh co' the^? dde^? cho ddo^'i phuo+ng ddi the^m nuo+'c ne^'u no' kho^ng to^'t ho+n beta hie^.n tho+`i thi` co' the^? cut off ngay.
Nhie^`u khi sau 2 loa.t nuo+'c kha'c nhau ke^'t qua?i ve^` mo^.t ba`n co+`. Gia? du. nhu+ mi`nh vo^ pha'o, le^n ma~ hay le^n ma~ vo^ pha'o thi` cu~ng nhu+ nhau tho^i. Trong truo+`ng ho+.p na`y mi`nh pha?i ti'nh gia' tri. 1 ba`n co+` nhie^`u la^`n.
Mo^.t ca'ch gia?i quye^'t la` mi`nh store ta^'t ca'c ba`n co+~ mi`nh va`o 1 hash table. Sau ddo' truo+'c khi dda'nh gia' mo^.t ba`n co+` na`o thi` mi`nh ti`m trong Hash table truo+'c. Ne^'u co' m`inh tra? ve^` gia' tri. ba`n co+` dda~ dduo+.c store trong hash table. Ne^'u kho^ng mi`nh mo+'i dda'nh gia'.
Thuo+`ng trong hash table nguo+`i ta cu~ng lu+u tru+~ va`o ddo' nuo+'c ddi to^''t nha^'t cu?a ba`n co+`. Ne^'u mo^.t ba`n co+` mi`nh muo^'n dda'nh gia' n+1 nuo+'c, ma` mi`nh dda~ co' no' trong hash table vo+'i gia' tri. to^'t nha^'t o+? <= n nuo+'c, thi` mi`nh cho.n nuo+'c ddi dda^`u tie^n la` nuo+'c ddi trong hash table, thi` alpha beta se~ dduo+.c cut off ra^'t mau cho'ng.
To'm la.i mo^~i pha^`n tu+? cu?a hash table la`:
struct hashEntry {
unsigned __int64 lock;
int value;
unsigned char bestX,bestY;
char flag;
char depth;
};
lock: (ddang suy nghi~ hehehe)
value, depth: Gia' tri. cu?a ba.n co+` sau khi ti'nh o+? ddo^. sa^u depth.
flag: DDo^i khi alphabeta kho^ng tra? ve^` gia' tri. thu+.c su+. cu?a ba`n co+` do bo+?i cut off. Lu'c na`y gia' tri. alphabeta chi? la` cha(.n tre^n hoa(.c cha(.n duo+'i ma` tho^i. Flag se~ cho mi`nh bie^'t gia' tri. cu?a ba`n co+` la` cha(.n tre^n, cha(.n duo+'i hay gia' tri. thu+.c su+..
bestX,bestY: Nuo+'c ddi to^' nha^'t cu?a ba`n co+`. Khi mi`nh tha^'y mo^.t ba`n co+` co' trong hash table, nuo+'c dda^`u tie^n mi`nh se~ thu+? la` nuo+'c ddi (bestX,bestY)
Pha't hie^.n su+. la^.p la.i: Nhu+~ng nuo+'c la^.p la.i co' ba('t qua^n hay chie^'u tuo+'ng la` kho^ng ho+.p le^. trong co+` tuo+'ng. Mi`nh co' the^? pha't hie^.n nhu+~ng nuo+'c la^.p la.i ba(`ng ca'ch so sa'nh nhu+~ng ba`n co+` vo+'i nhau (Phuo+ng pha'p na`y cha^.m) hay la` so sa'nh gia' tri. Hash cu?a ba`n co+`
Trong thu+.c te^', mo^~i nuo+'c pha?i suy nghi~ trong mo^.t tho+`i gian co^' ddi.nh, mi`nh kho^ng bie^'t pha?i search to+'i ddo^. sa^u bao nhie^u la` vu+`a. Mo^.t ca'ch gia?i quye^'t la` mi`nh search tu+` depth 1 tro+? ddi cho dde^'n khi he^'t gio+`. Ca'ch na`y co' lo+.i la` sau khi ti'nh nuo+'c thu+' n, mi`nh co' the^? sort ca'c move dde^? khi ti'nh nuo+'c n+1 ke^'t qua? nhanh cho'ng ho+n.
O+? giai ddoa.n khai cuo^.c, ma'y nghi~ ra^'t la^u vi` co' qua' nhie^`u nuo+'c ddi, mi`nh co' the^? lu+u mo^.t so^' the^' co+ ba?n cho ma'y ddi theo. Mu.c ddi'ch la` ta.o cho ma'y ddi nhu+~ng nuo+'c gio^'ng nguo+`i chu't ddi?nh.
Mo^.t ddie^?m nu+~a, khi computer thua 1 va'n thi` no' ra^'t kho+` thuo+`ng se~ ddi la.i nhu+~ng nuo+'c cu~. Cho ne^n mi`nh ne^n la`m ca'i open book sao cho kho^ng ddi la.i nhu+~ng va'n thua.
Vi` co`n i't qua^n ne^n mi`nh co' the^? la^.p mo^.t ca'i database dde^? lu+u ta^'t ca? ca'c ba`n co+`. Nhu+ng thangngo chu+a la`m dduo+.c ca'i na`y :-)
Ne^'u mi`nh co' tre^n hai CPu thi` la`m sao ta^.n du.ng dduo+.c ca? hai ??? DDang thu+? :-)
Computer Chess Programming dda^y la` ca'i home page co' nhie^`u link to+'i nhu+~ng cho^~ kha'c nha^'t.
Aske Plaat: MTD(f), a new chess algorithm mo^.t thua^.t toa'n nhanh ho+n alpha-beta ???
Machine Learning in Games ne^'u ma` vie^'t dduo+.c co+` tuo+'ng tu+. ho.c thi` he^'t sa^?y.